递归-回溯算法宇宙观（简单理解迷宫、皇后问题）

2019-11-14 | 阅读：次

递归-回溯算法宇宙观（简单理解迷宫、皇后问题）

最近在刷题的时候，对于一些使用递归的算法都不太理解，经常没有思路。经过刷了几个题，终于把抽象的递归形象化了，记录在此，帮助记忆。

很多递归的教程都是从斐波那契数列开始，但我想从一个更简单的题目开始切入。

题目为：给定一个整数n，请输出倒序再整数输出n~0,0~n，以空格分离。
示例，当n=1时，输出1, 0, 0, 1
当n=3时，输出3, 2, 1, 0, 0, 1, 2, 3

题目很简单，一般思路就是从n开始，循环递减打印，如下

// 打印数字
public static void printNum(int n) {
    for (int i = n; i >=0; i--) {
        System.out.print(i + " ");
    }
    for (int i =0; i <= n; i++) {
        System.out.println(i + " ");
    }
}

这么写完全正确，那如果用递归来写怎么实现呢？下面这样写对吗？

public class MyTest{

    public static void main(String[] args) {
        printNum(3);
    }

    // 打印数字
    public static void printNum(int n) {    // 第8行
        // n小于0，不打印了，返回
        if (n < 0) {
           return;
       }
       System.out.print(n + " "); // 第13行
       n--;
       printNum(n); // 第15行
       System.out.println(n + " "); // 第16行
    }
}

上面代码的控制台输出是，显然代码是错的：

3 2 1 0 -1 0 1 2

我们来看看为什么会导致这个错误，代码第15行之前这些这些代码虽然是递归，但是按人类正常顺序思路来看，很容易理解。在第8行printNum这个方法中，当n=5时，先打印数字5，第14行减1，第15行再递归打印数字4，以此类推，直到小于0则不打印了，此时栈中的各个方法应该执行第16行。第15行以后就不好理解了，为什么打印了-1呢？

递归的宇宙

为了便于理解递归，我们定义一个方法宇宙的概念。我们知道，每个方法调用的时候都用各自的栈空间，方法返回则栈销毁。如此，我们不就可以将一个方法看成一个宇宙，方法内的代码在这个宇宙中运行，方法返回宇宙消失。

递归递归，顾名思义，分为递和归两个过程

历史宇宙

如此，再来理解上面的代码。假设当n=3，起初，代码在第8行和第15行之间一直递归，我们把递归看成历史宇宙，代码运行逻辑：（递）n=3历史宇宙里打印了数字3 => n=2历史宇宙里打印数字2 => n=1历史宇宙里打印了数字1 => n=0历史宇宙打印了数字0 => n=-1的宇宙直接返回了 => （printNum执行完，归） => n=0历史宇宙第十四行执行了n–，故第十六行打印-1 => n=1宇宙同理，打印0。

找到原因，这时我们知道怎么改了，因为第14行代码将n–了，所以第15行历史宇宙回归后，我们需要加回来，即n++。代码改为如下：如下添加了第16行。

public class MyTest{

    public static void main(String[] args) {
        printNum(3);
    }

    // 打印数字
    public static void printNum(int n) { // 第8行
        // n小于0，不打印了，返回
        if (n < 0) {
           return;
       }
       System.out.print(n + " "); // 第13行
       n--;
       printNum(n); // 第15行
       n++; // 第16行
       System.out.print(n + " "); // 第17行 
    }
}

输出正如我们所料，如下：

3 2 1 0 0 1 2 3

得出结论，整个方法是一个宇宙，第15行printNum方法之前是递的过程，通过第15行printNum方法进到历史宇宙最深处，第15行后是在每个历史宇宙做的事，事情做完回归。如下图：

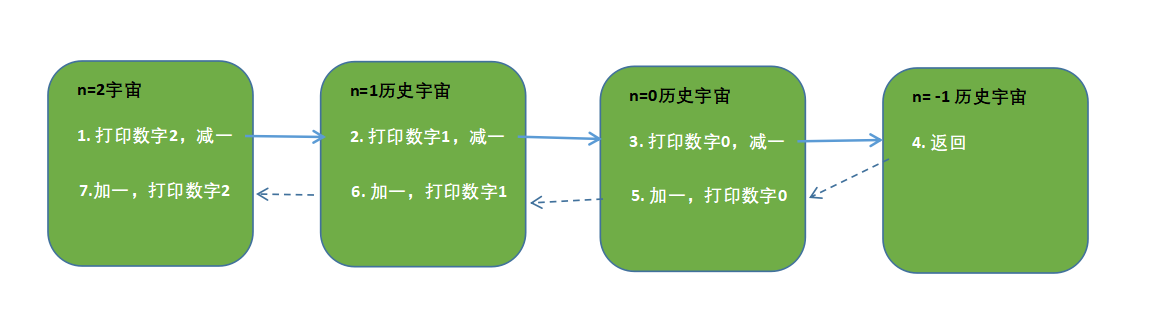
如此，甚至能在0号历史宇宙做的手脚呢？如下，在0号历史宇宙打印一句话。

public class MyTest{

    public static void main(String[] args) {
        printNum(3);
    }

    // 打印数字
    public static void printNum(int n) { // 第8行
        // n小于0，不打印了，返回
        if (n < 0) {
           return;
       }
       System.out.print(n + " "); // 第13行
       n--;
       printNum(n); // 第15行
       n++; // 第16行
       System.out.print(n + " "); // 第17行 
       if (n == 0) {
           System.out.print("++我在0历史宇宙，我要回归啦++ ");
       }
    }
}

如上代码，输出如下：

3 2 1 0 0 ++我在0历史宇宙，我要回归啦++ 1 2 3

平行宇宙

除了历史宇宙，我们还能通过循环，进入平行宇宙。假如我们要在1号宇宙的时候，再分化出一个平行宇宙，怎么做呢？代码如下：

public class MyTest{

    public static void main(String[] args) {
        printNum(3);
    }

    // 打印数字
    public static void printNum(int n) { // 第8行
        // n小于0，不打印了，返回
        if (n < 0) {
           return;
       }
       System.out.print(n + " "); // 第13行
       n--;
       // 1号宇宙分化出一个平行宇宙，再进入历史宇宙
       if (n == 1) {
            for (int i =0; i < 2; i++) {
                printNum(n);
            }
       }else {
           printNum(n);
        // 其他号宇宙进入历史宇宙
       }
       n++; 
       System.out.print(n + " "); 
        if (n == 0) {
            System.out.print("++我在0历史宇宙，我要回归啦++ ");
        }
    }
}

输出如下，应该能看懂吧。

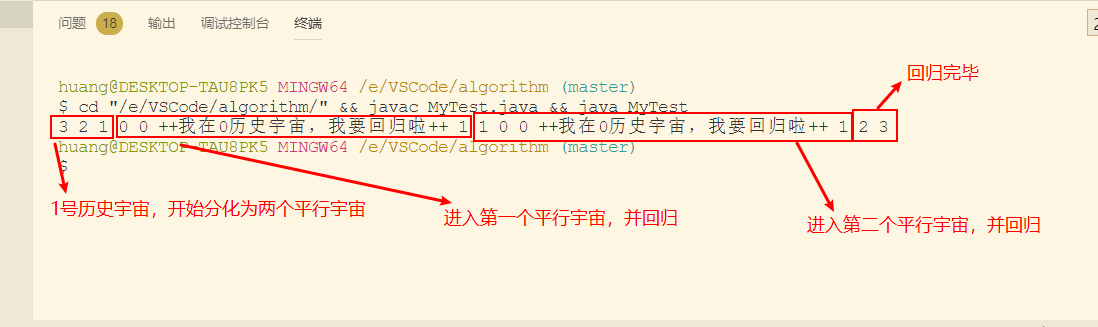
回溯算法

回溯算法可谓算法编程中的暴力美学啊，其本质就是通过DFS(深度优先遍历)枚举了问题中的所有情况，然后记录满足你的问题的解。回溯算法通过一步步试错，这一次走这条路，如果错了则倒退，走另外一条路，遍历完所有可能。为什么能回溯呢？不正好是递归里面的穿梭到历史宇宙再回来的情况吗。

回溯算法之所以能回溯撤退的原因，是因为递归能自动回退

迷宫问题

以一个9*8的长方阵表示迷宫，1表示迷宫中的通路、0表示障碍。入口为左上角，出口为右下角。设计程序，求出从入口到出口的所有通路。
{1, 1, 0, 1, 1, 1, 0, 1},
{1, 1, 0, 1, 1, 1, 0, 1},
{1, 1, 0, 1, 0, 0, 1, 0},
{1, 0, 0, 0, 1, 1, 0, 1},
{1, 1, 1, 0, 1, 1, 1, 1},
{1, 0, 1, 1, 1, 0, 1, 0},
{1, 0, 0, 0, 0, 1, 1, 0},
{0, 0, 1, 1, 1, 0, 1, 0},
{0, 0, 1, 1, 1, 1, 1, 1}

题目要求找出所有的通路，很明显，需要遍历整个迷宫，适合使用回溯算法。我们的思路是，从左上角开始，在每个宇宙里，都往上下左右四个方向走，首先一直往右走，每往前走一步时，先查查右边能否走通，走不通则走另外三个方向，走过的路则标记为数字6。代码如下，注意看注释。

public class MazeTest{

    //  迷宫，9行8列
    private static int ROW = 9;
    private static int COLUMN = 8;
    private static int[][] maze = {
        {1, 1, 0, 1, 1, 1, 0, 1},
        {1, 1, 0, 1, 1, 1, 0, 1},
        {1, 1, 0, 1, 0, 0, 1, 0},
        {1, 0, 0, 0, 1, 1, 0, 1},
        {1, 1, 1, 0, 1, 1, 1, 1},
        {1, 0, 1, 1, 1, 0, 1, 0},
        {1, 0, 0, 0, 0, 1, 1, 0},
        {0, 0, 1, 1, 1, 0, 1, 0},
        {0, 0, 1, 1, 1, 1, 1, 1}
    };


    public static void main(String[] args) {
        
        // 从左上角开始走迷宫
        walk(0, 0);
    }

    public static void walk(int i , int j){

        // 如果到达右下角，说明该路线可以走通
        if (i >= ROW-1 && j >= COLUMN-1) {
            //  打印当前迷宫痕迹
            System.out.println("找到一种解法如下：====");
            for (int r = 0; r < ROW; r++) {
                for (int c = 0; c < COLUMN; c++) {
                    System.out.print(maze[r][c]);
                }
                System.out.println();
            }
            return;
        } // ===打印迷宫结束

        // 向右走，先查查是否可以站在这个i, j+1 这个点上
        if (canStand(i, j+1)) {
            // 可以站在这个点上，站上去（标记已走过）
            maze[i][j] = 6;
            walk(i, j+1); // 往右走，进入下一个历史宇宙
            // 在最右边历史宇宙撞墙了，这个宇宙上面把这个点改为6了，需要改回来，否则篡改历史，会引发未知的蝴蝶效应
            maze[i][j] = 1;
        }

        // 在最右历史宇宙中走不下去，向下走
        if (canStand(i+1, j)) {
            maze[i][j] = 6;
            walk(i+1, j);
            maze[i][j] = 1;
        }

        // 向左走
        if (canStand(i, j-1)) {
            maze[i][j] = 6;
            walk(i, j-1);
            maze[i][j] = 1;
        }

        // 向上走
        if (canStand(i-1, j)) {
            maze[i][j] = 6;
            walk(i - 1, j);
            maze[i][j] = 1;
        }

    }

    private static boolean canStand(int i, int j) {
        //System.out.print("[" + i + "," + j + "]=>");
        //  走到边界了
        if (i >= ROW || j >= COLUMN || i < 0 || j < 0) {
            return false;
        }

        // 遇到障碍了
        if (maze[i][j] == 0) {
            return false;
        }

        // 走过了
        if (maze[i][j] == 6) {
            return false;
        }
        return true;
    }
}

上面代码8种走法，输出结果为：

找到一种解法如下：====
66011101
16011101
66010010
60001101
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
66011101
16011101
66010010
60006601
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
66011101
66011101
61010010
60001101
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
66011101
66011101
61010010
60006601
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
61011101
66011101
66010010
60001101
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
61011101
66011101
66010010
60006601
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
61011101
61011101
61010010
60001101
66606661
10666060
10000160
00111060
00111161
找到一种解法如下：====
61011101
61011101
61010010
60006601
66606661
10666060
10000160
00111060
00111161

如上，在入口(0, 0)处，可以往右或者往下，我们先一直往右走，碰到墙时，在最右的历史宇宙中往下走，再往右走。最后回溯到最左的入口历史宇宙时，会尝试往下走的做法。故可以完成遍历。